Reduction And Intractibility

Complexity Classes

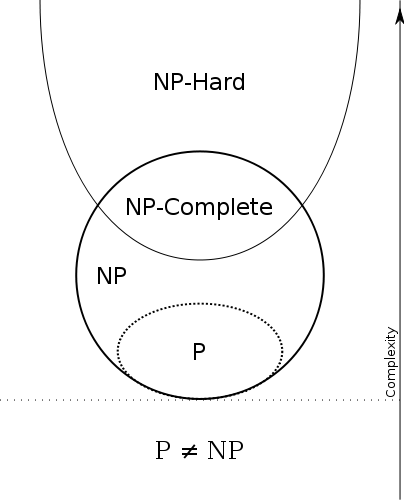
With complexity classes, we aim to determine the “difficulty” of a problem. They allow us to know what is solvable in polynomial time and what isn’t. This is what the $P = NP$ problem deals with. $P=NP$ implies that for any polynomial time verification solution, there is a polynomial time solver for the problem. Most computer scientists believe that $P \neq NP$. Assuming $P \neq NP$,

P

Loosly, $P$ is defined as the set of all problems such that there is a polynomial time solution. This means that the solution to a problem $a \in P$ runs in $O(n^k)$ time where $k$ is some constant.

NP

Loosly, $NP$ is defined as the set of all problems such that there is a polynomial time verification.

NP-Hard

Loosly, $NP-Hard$ problems are such that any problem in $NP$ can be reduced to that $NP-Hard$ problem. Notice that the problen need not be in $NP$. We have a special class of problems for those, as seen below.

NP-Complete

Loosly, $NPC$ problems are considered the hardest problems in $NP$. Basically, any problem in $NP$ can be reduced to a $NPC$ problem. This means that any $NPC$ problem can be reduced to another $NPC$ problem. As you can see $NPC \subset NP-Hard$

Reductions

Reductions allow us to to determine the difficulty of a problem.

We say that for two problems $Y$ and $X$, $Y \leq_p X$ if instances of $Y$ can be solved by a polynomial amount of computation plus a polynomial number of calls to a “black-box” that solves $X$.

You can think of reduction as calling a library as part of your solution. For example.

In order for reductions to work, we have to have some set of problems that are known to be $NPC$. A common starting point is $SAT$, or boolean satisfiability. Karp has a famous paper containing 21 $NPC$ problems you can view here. Here are some popular $NPC$ Problems

3SAT

For $3SAT$, we are given a boolean formula $\Phi$ in CNF form (conjunctive normal form) such that for each clause $C_r$, $C_r = l_1 \lor l_2 \lor l_3$. We return true if this boolean formula is satisfiable.

Clique

We say that a graph $G$ has a clique of size $k$ if there is a set of vertices $I$ such that $\left\vert{I}\right\vert = k$ and $I$ is fully connected.

We will give a reduction from $CLIQUE$ to $3SAT$.

We can define our function $A$ as follows:

For each $C_r = ( l_1 \lor l_2 \lor l_3)$ for $r =1,\ldots,k$ , create corresponding vertices $v_1, v_2, v_3$ in $V$. Now add an edge between $v_i^r$ and $v_j^s$ if $r \neq s$ and the corresponding literals are consistent( You can’t connect $\neg l_1$ to $l_1$). Now we se that if there is a clique of size $k$, there is a satisfiable boolean formula for 3SAT.

Vertex Cover

We will prove that $VERTEX\ COVER \leq_p CLIQUE$.

We say that a graph $G = (V,E)$ has a vertex cover of size $k$ if there is a subset of vertices $S \subset V$ that covers all edges in the graph and $\left\vert{S}\right\vert = k$.

Given a graph $G = (V,E)$, we can generate the complement graph $\bar{G} = (V, \bar{E})$. Now, we solve the problem $CLIQUE(\bar{G}, \left\vert{V}\right\vert - k)$, and return $YES$ if we have a solution, and $NO$ otherwise.

You can see a full proof here