Genetic Algorithms

Creating a genetic algorithm that generates an expression that evaluates to 42.

The Problem

So I’ve been meaning to create a blog to chronicle all the technical stuff I do, and I just discovered jekyll-now and I love it so far. So without much further ado, this is the first post on my blog, and it describes running a genetic algorithm to create a string of numbers and operations that evaluates to 42.

For example, when I run the algorithm, one string it may return is \(262-12-246\). It’s important to note that the string that it does return will always be “gramatically” correct - it will always be formatted properly (for example, there wont be something like \(2++34\))

The Approach

The idea is to mimic biological natrual selection acting on a population of organisms. Each individual of the population has a fitness score, which I have defined in my code as the distance from the result of that expression to 42. An individuals chance to reproduce to pass on its genetic information to the next generation is directly tied to this fitness score. The process of reproduction has two opportunities for change - recombination and mutation.

• Recombination is when two organisms share their genes when they mate and the offspring recieves half the genes from one parent and half the genes from another. This is analogous to chromosomal crossover
• Mutation is the altering of a gene when it is copied and is much less common.

Basically, we simulate a population and make it reproduce until we get the result we want, or the entire population dies out.

More Theory

Recombination Visualized

Parent 1: 00000000000000000
Parent 2: 11111111111111111

Offspring: 0000001111111111

Mutation Visualized

Parent 1: 00000000000000000
Parent 2: 00000000000000000

Offspring: 0000000000010000

How we select the next generation

Basically, we use something called the roulette wheel method, where an individuals chance of getting selected is equal to

This will probably be more about the code that runs, rather than the theory behind it all. I encourage you to check out this site for more information.

The Code

Creating the population and enviorment

We need to first develop a way for us to store genetic information. For that, we use a bitstring that is 36 bits long. We also create an encoding for our information.

encoding = {
        '0000' : '0',
        '0001' : '1',
        '0010' : '2',
        '0011' : '3',
        '0100' : '4',
        '0101' : '5',
        '0110' : '6',
        '0111' : '7',
        '1000' : '8',
        '1001' : '9',
        '1010' : '+',
        '1011' : '*',
        '1100' : '-',
        '1101' : '/',
        '1110' : '1', #extra encodings for 0, 1
        '1111' : '2',
}

The next thing to do is to randomly create chromsomes for our population. To do this, I used this line of code

for i in range(0,popSize):
    s = bin(random.randint(0, math.pow(2, 4*expLength)))[2:].zfill(4*expLength);

Basically it creates a random number from \(0\) to \(2^{36}\), and then calls bin() on the output, which returns something like 0b01001010010, from which we just grab the binary bits and then right fill with 0’s to ensure all outputs are the same length.

Determining the fitness of an individual.

I first checked if the string evaluated to a valid expression - otherwise the fitness score was 0. If the string was a valid expression, then the function evaluates the expression and then uses this function to determine the fitness

def evaluateChromosome(bitstring):
    expression = [encoding[bitstring[i:i+4]] for i in range(0, len(bitstring), 4)];

    if expression[0] in operators or expression[-1] in operators:
        return 0;

    #making the stacks
    numbers=[];
    operations=[];
    numString="";
    needOperand=False;

    for c in expression:
        if needOperand and c in operators:
            return 0;
        elif needOperand and c in operands:
            needOperand = False;

        if c in operands:
            numString+=c;
        else:
            needOperand = True;
            operations.append(c);
            if len(numString) != 0:
                numbers.append(int(numString));
            numString = "";

    if len(numString) != 0:
        numbers.append(int(numString));

    #evaluating the stacks
    while len(operations)!=0:
        num1 = numbers.pop(0);
        num2 = numbers.pop(0);
        op=operations.pop(0);

        if op == '+':
            numbers.insert(0, num1+num2);
        elif op == '*':
            numbers.insert(0, num1*num2);
        elif op == '-':
            numbers.insert(0, num1-num2);
        elif op == '/':
            if num2 == 0:
                return 0;
            numbers.insert(0, num1/num2);

    if numbers[0] == 42:
        print("FOUND EXPRESSION:  "  + "".join(expression));
        input("Press Enter to continue...");
        quit();

    return abs(1/(42-numbers[0]));

Running the Simulation

I wrote a simple iterator for the program to create two children for each set of parents

def iterateGeneration(i):
    #weight parameters
    global population
    temppopulation={};
    total = sum(population.values());
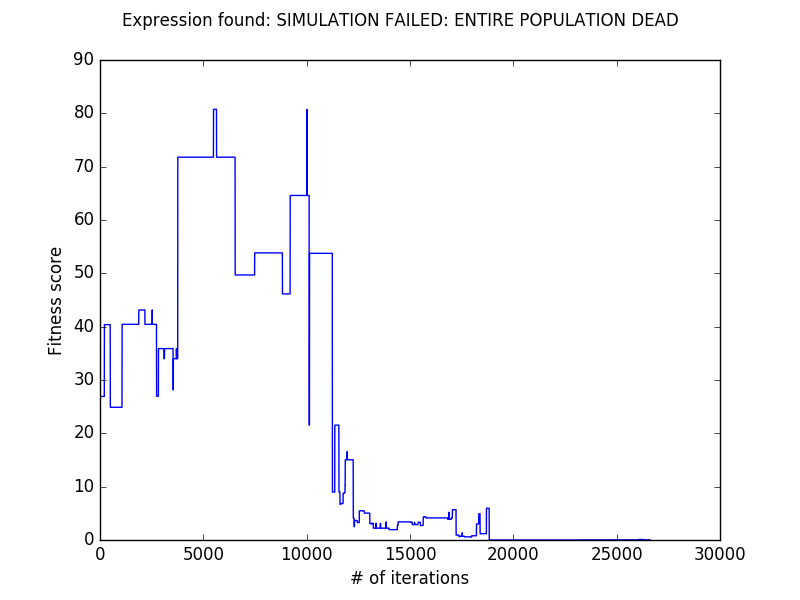
    if total ==0:
        print("SIMULATION FAILED: ENTIRE POPULATION DEAD");
        input("Press Enter to continue...");
        quit();

    for s in population:
        population[s] /= total;
    for j in range(0, len(population), 2):
        p1 = np.random.choice(list(population.keys()),p=list(population.values()));
        p2 = np.random.choice(list(population.keys()),p=list(population.values()));

        offspring1, offspring2 = breedOffspring(p1,p2);
        temppopulation[offspring1] = evaluateChromosome(offspring1);
        temppopulation[offspring2] = evaluateChromosome(offspring2);

    population =temppopulation;

    print("Iteration " + str(i) + ": Best bitstring and value are");
    
    bitstring = max(population, key=lambda x: population[x]);
    print(bitstring);
    print([encoding[bitstring[i:i+4]] for i in range(0, len(bitstring), 4)]);
    print(population[bitstring]);

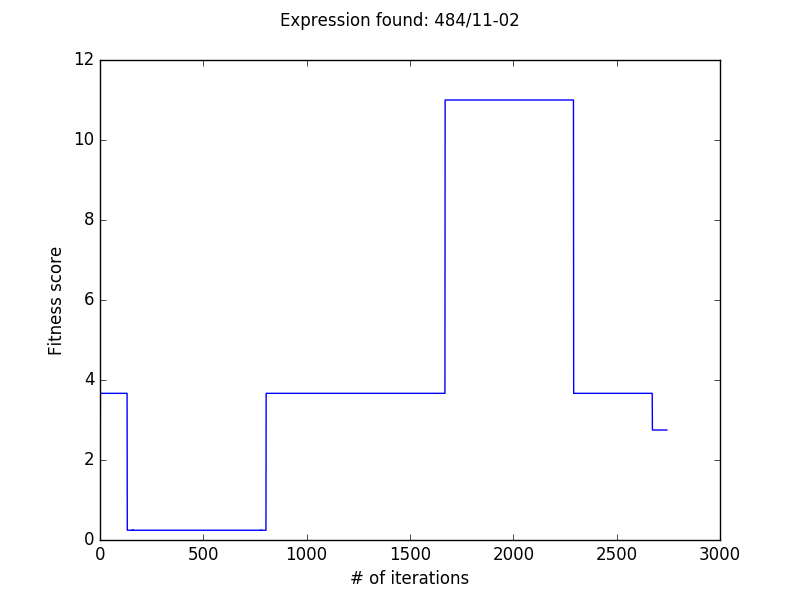
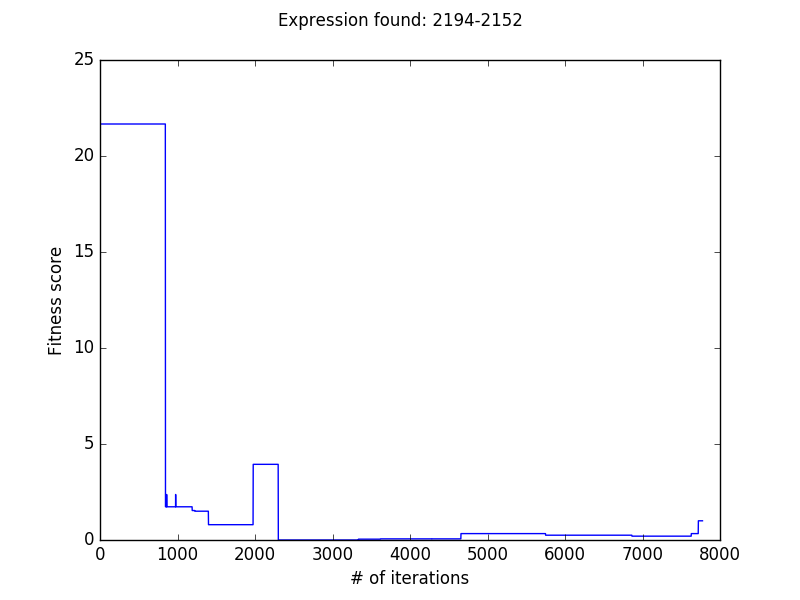
The Result

It works!!! I think this is super cool for a little work. I wrote a simple mpl function to display the result: This was super fun! See the rest of the code here.