Generative Models

I’m going to be doing a series of blog posts about generative models, and how one can use them to tackle semi-supervised learning problems. In this post I’m going to go over PixelRNN/CNN, a generative model that

Generative models can be thought of a form of unusupervised learning or density estimation. We are trying to model the underlying distribution from the data.

They can be used for super-resolution, colorization, and simulation.

Explcit density estimation - explicitly define and solve for \(p_{model}(x)\)

Implicit density estimation - learn a model to produce models from \(p_{model}(x)\) without explicityl defining it.

PixelRNN/CNN

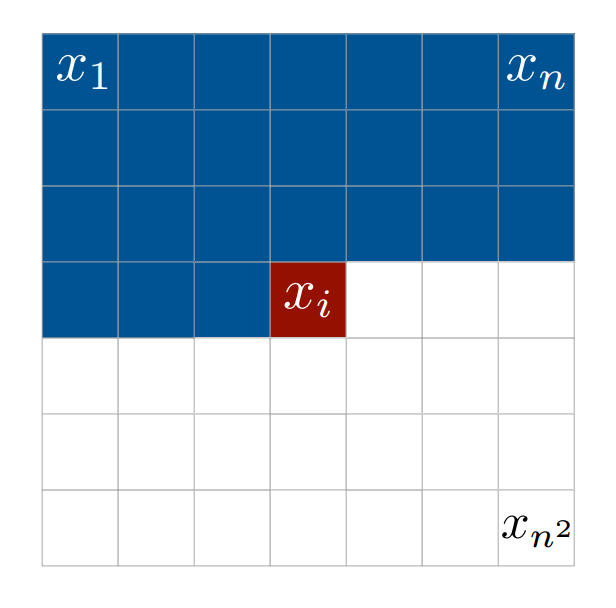
The idea here is to go through each pixel, row by row, and use a recurrent neural network in order to generate a conditional probability distribution over the possible pixel values.

This is a tractable explicit model that is a type of fully visible belief network.

\[p(x) = \prod_{i=1}^n p(x_i \vert x_1 \ldots x_{i-1})\]

We train this using MLE, maxamizing the likelihood of the training data. Use neural netowrk to express the distribution.

Will need to define the ordering of pixels - starting from the corner. Each dependency is modeled via a LSTM RNN.

However, this means that our training is very slow, as each pixel depends on the previous pixels for the hidden vector.

PixelCNN - uses the same approach as PixelRNN, but the dependency is now codified by a CNN over a specified context region.

Train using MLE - output is a softmax loss at each pixel. Max the likelihood that our training data is generated.

Training is faster than PixelRNN, we can also parallelize convolutions. However, generation is still slow, as it is sequential.

Chain rule basically defines a tractable density that is easy to work with. Gives a good evaluation metric of our data via the training likelihood.